u-Substitution: My Very First Pullback

You usually hear about pullbacks in advanced calculus, but we’ve already snuck one by you in calc 1. Let me show you where.

Contents:

• The setup
• Going fast
• Pullbacks galore
• Reverse chain rule

The setup

1. Walk along the $x$ axis.
2. Stop for a sec every once in while and calculate $f(x)$.
3. Sum up the areas of some (red) rectangles.

4. Do step 2. often enough and you get

   $${\int }_a^{b}f(x)dx\approx \sum f(x_i)\mathrm{\Delta }{x}_i.$$

Try it out live:

Accuracy: High Avg Low

Speed: Constant Roller coaster

Going fast

Stopping every $\mathrm{\Delta }{t}_i$ seconds (this is the once in a while from step 2.) is really easy, just keep an eye on your watch. On the downside, there’s the side effect that the rectangle bases are uneven when we speed up or slow down. We can fix the aesthetics by bringing time front and center.

Accuracy: High Avg Low

Speed: Constant Roller coaster

$$\sum_{i=1}^{0} f(x(t_i))\Delta t_i = 0.00$$

$$\sum_{i=1}^{0} f(x)\Delta x_i = 0.00$$

Somewhat surprisingly, the blue and the red rectangles give us different numbers. What went wrong? We slowed down at the top to look at the view, but the relevant blue rectangle doesn’t know we haven’t moved much during his $\mathrm{\Delta }{t}_i$ (Time waits for no one…). Conveniently, his red friend knows exactly how much we moved during that time, it’s his $\mathrm{\Delta }{x}_i$.

You might want to click a rectangle up there right now.

Let’s redo the sum with this new information.

$$\sum_{i=1}^{0} f(x(t_i))\frac{\color{#ff6d6d} {\Delta x_i}}{\color{#569AFF}{\Delta t_i}}\Delta t_i = 0.00$$

$$\sum_{i=1}^{0} f(x_i)\Delta x_i = 0.00$$

This time, each blue rectangle reminded us how much $x$ we moved during his $\mathrm{\Delta }{t}_i$. It momentarily expanded\contracted to the right size by multiplying its base by $\frac{\mathrm{\Delta }{x}_i}{\mathrm{\Delta }{t}_i}$ and then snapped back once we were done with it. this gave us the right number:

$$\sum f(x(t_i))\frac{\mathrm{\Delta }{x}_i}{\mathrm{\Delta }{t}_i}\mathrm{\Delta }{t}_i=\sum f(x_i)\mathrm{\Delta }{x}_i.$$

At the limit $\mathrm{\Delta }{t}_i\to 0$ this becomes integration by substitution:

$${\int }_{x^{-1}(a)}^{x^{-1}(b)}f(x(t))x^{\prime }(t)dt={\int }_a^{b}f(x)dx.$$

Pullbacks galore

We moved geometric information (about lengths of $\mathrm{\Delta }{x}_i$’s) from the world of $x$ back to the world of $t$. The jargon for this is pullback and it shows up everywhere once you start looking. Start looking here:

• You’ve used a map with a scale, so now you know. In this case the map pulls back lengths from the actual world to the paper it’s printed on.

  

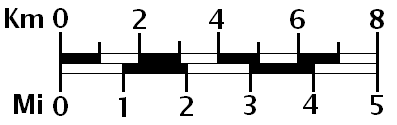
  A pullback
• For really good maps, this 1d scale doesn’t cut it anymore. You need to pull back a metric tensor. The first 10 mins of this video are a great intro, though it picks up speed afterwards.
• Steve Mould has some other, physics inspired examples.

Reverse chain rule

Summing rectangles is cute, but you should check out the proof [Wiki]. It’s a one liner using the chain rule:

$$\frac{df}{dt}=\frac{df}{dx}\frac{dx}{dt}.$$

You understand this one intuitively if you’ve ever switched gears in a car. If not, check out the viz here.